Step-by-Step Guide to Dynamic Programming Examples
Dynamic Programming (DP) solves complex problems by breaking them down into simpler subproblems. It is widely used in mathematics, computer science, and operations research. This technique ensures that each subproblem is only solved once, saving time and computational resources. This guide will provide a comprehensive overview of dynamic programming with detailed examples to enhance your understanding.
Understanding Dynamic Programming
Dynamic programming is based on the principle of optimality, which asserts that the optimal solution to any instance of an optimization problem comprises optimal solutions to its subproblems. DP exploits this recursive property to decrease computation time by storing intermediate results.
The two main approaches to implementing dynamics are:
- Top-Down Approach (Memoization): This approach involves writing the recursive algorithm first and then improving its efficiency by storing the results of intermediate subproblems to avoid recomputation.
- Bottom-Up Approach (Tabulation): In this approach, the problem is solved by first looking at the smaller subproblems and then solving larger subproblems using the solution of the previous subproblems.
Dynamic Programming Examples
To illustrate how dynamic programming works, let’s explore some classic dynamic programming examples.
Example 1: Fibonacci Sequence
The Fibonacci sequence is a famous example of how dynamic programming can be effectively utilized. The sequence is defined by the recurrence relation:
????(????)=????(????−1)+????(????−2)
with initial conditions ????(0)=0 and ????(1)=1.
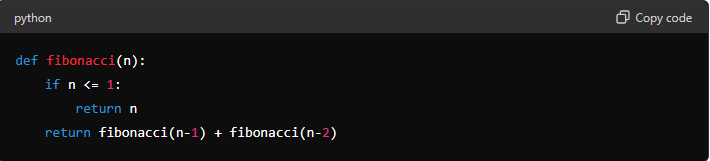
Naive Recursive Solution:
Dynamic Programming Solution:
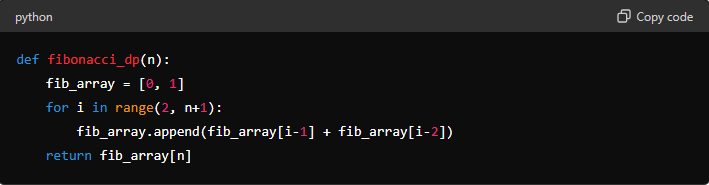
By storing the results of the Fibonacci numbers as we compute them, we prevent the exponential blow-up in the computation time that occurs in the naive recursive approach.
Example 2: 0/1 Knapsack Problem
The 0/1 Knapsack problem is a popular problem where you are given a set of items, each with a weight and a value, and a knapsack with a capacity. The goal is to determine the number of each item to include in the collection so that the total weight is less than or equal to the knapsack’s capacity and the total value is as large as possible.
Dynamic Programming Solution:
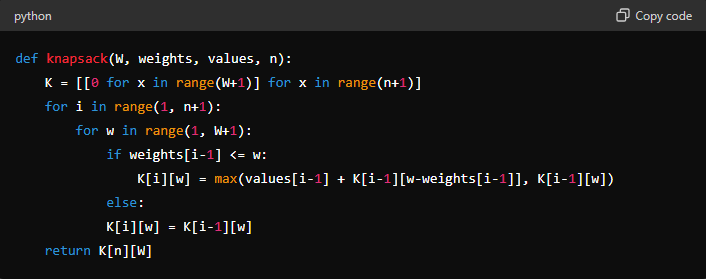
In this example, the ‘K[i][w]' table is used to store the maximum value that can be achieved with the first ‘i' items and a knapsack capacity of ‘w'.
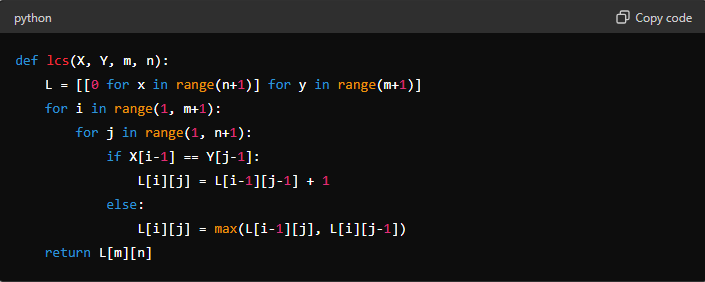
Example 3: Longest Common Subsequence
The problem of finding the longest common occurrence (LCS) is another classic example of dynamic programming’s usefulness. Given two sequences, the task is to find the longest subsequence in both.
Dynamic Programming Solution:
Example 4: Coin Change Problem
The Coin Change problem involves finding the number of ways to make a certain amount of money with a given set of coins. It’s a fundamental problem for understanding how to use dynamic programming to solve counting problems.
Dynamic Programming Solution:
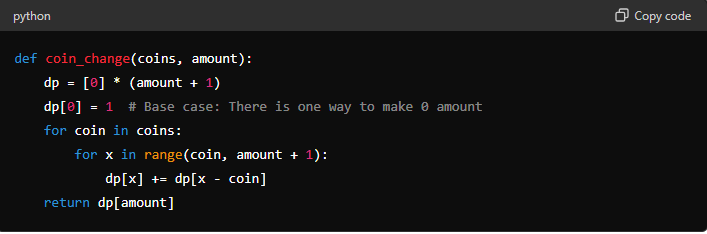
This solution initializes an array ‘dp' where each index 'x' holds the number of ways to create the value ‘x'. By iterating over all coins and updating the dp array, it builds up the number of ways to form each amount up to the target.
Example 5: Minimum Path Sum in a Grid
Given a grid filled with non-negative numbers, find a path from the top left corner to the bottom right corner which minimizes the sum of the numbers along its path. You can only move either down or right at any point in time.
Dynamic Programming Solution:
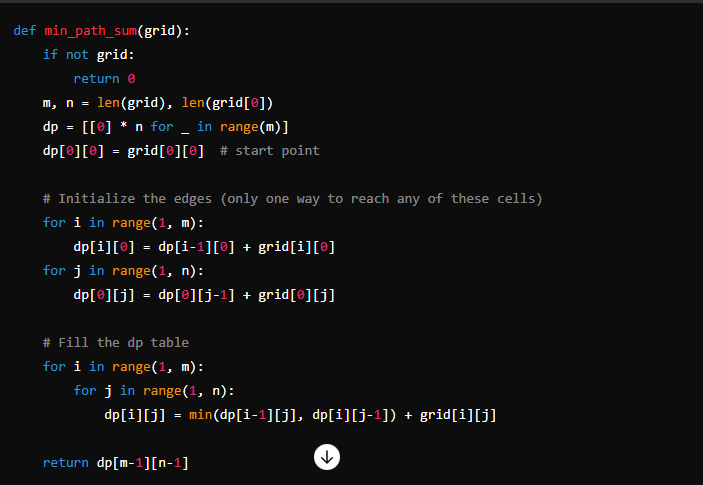
This example uses a 2D ‘dp' array where ‘dp[i][j]' represents the minimum path sum to reach cell ‘(i, j)' From the top left corner. The value at each cell is calculated as the minimum of the two possible preceding cells plus the current cell’s value.
Example 6: Edit Distance (Levenshtein Distance)
The Edit Distance problem measures the minimum number of operations required to convert one string into another, where the operations can be insertions, deletions, or substitutions of characters.
Dynamic Programming Solution:
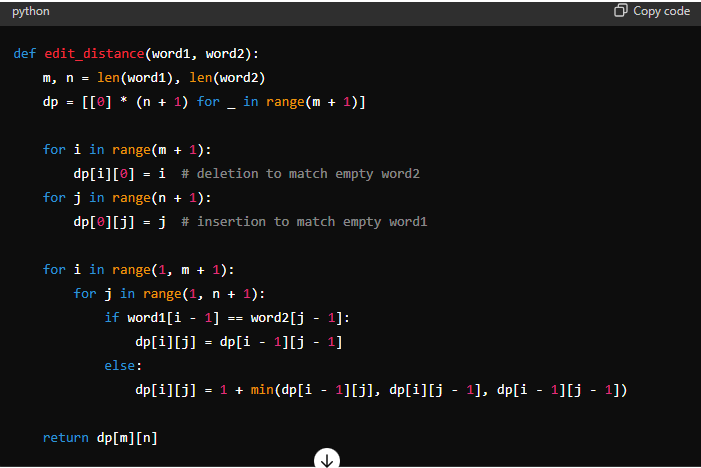
This example utilizes a matrix dp where ‘dp[i][j]' represents the minimum edit distance between the first ‘i' characters of ‘word1' and the first ‘j' characters of ‘word2'. The matrix is filled by considering all possible operations that can convert ‘word1' to ‘word2'.
Best Practices and Tips
- Identify the Subproblems: In dynamic programming, the first step is to identify how to break the problem into subproblems.
- Decide on a Recurrence Relation: Every DP solution requires you to find a way to relate the problem’s solution to its subproblems.
- Initialize the DP Array: Correct initialization is crucial to ensure that the base cases are handled properly.
- Iterative vs. Recursive: Iterative solutions (bottom-up) are usually more space-efficient than recursive solutions (top-down) because they avoid recursion overhead.
Conclusion
Dynamic programming is a powerful technique that can significantly speed up the computation of problems involving sequential decision-making. Mastering dynamic programming enables you to tackle a wide range of problems more efficiently. Whether you are preparing for competitive programming, coding interviews, or working on complex algorithmic challenges, understanding dynamic programming is an invaluable skill.
Read Dive is a leading technology blog focusing on different domains like Blockchain, AI, Chatbot, Fintech, Health Tech, Software Development and Testing. For guest blogging, please feel free to contact at readdive@gmail.com.
